1386. Cinema Seat Allocation

1386. Cinema Seat Allocation

A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i]=[3,8] means the seat located in row 3 and labelled with 8 is already reserved. 

Return the maximum number of four-person families you can allocate on the cinema seats. A four-person family occupies fours seats in one row, that are next to each other. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be next to each other, however, It is permissible for the four-person family to be separated by an aisle, but in that case, exactly two people have to sit on each side of the aisle.

Example 1:

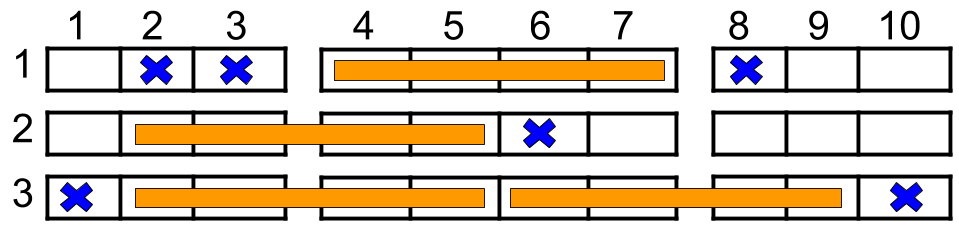
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four families, where seats mark with blue are already reserved and contiguous seats mark with orange are for one family. 

Example 2:

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

class Solution {
public:
    int maxNumberOfFamilies(int n, vector<vector<int>>& r) {
        unordered_map<int,vector<int>> m;
        for(auto& x:r){
            m[x[0]-1].push_back(x[1]-1);
        }
        int total=(n-m.size())*2;
        for(auto it=m.begin();it!=m.end();it++){
            total+=countSeats(it->second);
        }
        return total;
    }
    int countSeats(vector<int> rSeats){
        vector<int> seats(10,0);
        for(int i=0;i<rSeats.size();i++){
            seats[rSeats[i]]=1;
        }
        //012 3456 789
        int cntLeft=0;
        int cntRight=0;
        int cntCenter=0;
        for(int i=1;i<=8;i++){
            if(i<=4&&seats[i]==0){
                cntLeft++;
            }
            if(i>=5&&seats[i]==0){
                cntRight++;
            }
            if(i>=3&&i<=6&&seats[i]==0){
                cntCenter++;
            }
        }
        if(cntLeft+cntRight==8){
            return 2;
        }
        else if(cntLeft==4||cntRight==4||cntCenter==4){
            return 1;
        }
        
        return 0;
    }
};